2054. 两个最好的不重叠活动

🟠   🔖  数组 二分查找 动态规划 排序 堆（优先队列）  🔗 力扣 LeetCode

题目

You are given a 0-indexed 2D integer array of events where events[i] = [startTimei, endTimei, valuei]. The ith event starts at startTimei and ends at endTimei, and if you attend this event, you will receive a value of valuei. You can choose at most two non-overlapping events to attend such that the sum of their values is maximized.

Return thismaximum sum.

Note that the start time and end time is inclusive : that is, you cannot attend two events where one of them starts and the other ends at the same time. More specifically, if you attend an event with end time t, the next event must start at or after t + 1.

Example 1:

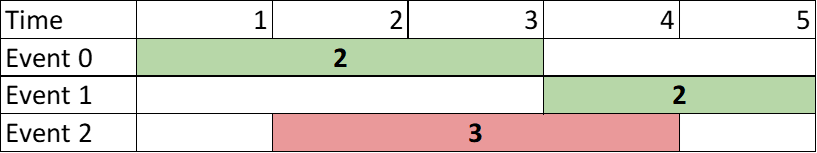
Input: events = [[1,3,2],[4,5,2],[2,4,3]]

Output: 4

Explanation: Choose the green events, 0 and 1 for a sum of 2 + 2 = 4.

Example 2:

Example 1 Diagram

Input: events = [[1,3,2],[4,5,2],[1,5,5]]

Output: 5

Explanation: Choose event 2 for a sum of 5.

Example 3:

Input: events = [[1,5,3],[1,5,1],[6,6,5]]

Output: 8

Explanation: Choose events 0 and 2 for a sum of 3 + 5 = 8.

Constraints:

• 2 <= events.length <= 10^5
• events[i].length == 3
• 1 <= startTimei <= endTimei <= 10^9
• 1 <= valuei <= 10^6

题目大意

给你一个下标从 0 开始的二维整数数组 events ，其中 events[i] = [startTimei, endTimei, valuei] 。第 i 个活动开始于 startTimei ，结束于 endTimei ，如果你参加这个活动，那么你可以得到价值 valuei 。你 最多 可以参加 两个时间不重叠 活动，使得它们的价值之和 最大 。

请你返回价值之和的 最大值 。

注意，活动的开始时间和结束时间是 包括 在活动时间内的，也就是说，你不能参加两个活动且它们之一的开始时间等于另一个活动的结束时间。更具体的，如果你参加一个活动，且结束时间为 t ，那么下一个活动必须在 t + 1 或之后的时间开始。

示例 1:

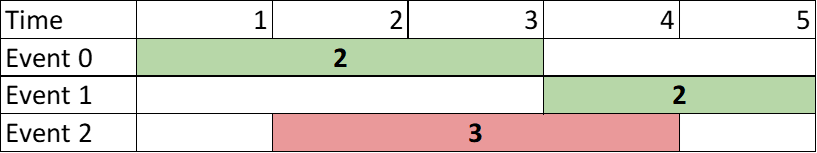
输入： events = [[1,3,2],[4,5,2],[2,4,3]]

输出： 4

解释： 选择绿色的活动 0 和 1 ，价值之和为 2 + 2 = 4 。

示例 2：

Example 1 Diagram

输入： events = [[1,3,2],[4,5,2],[1,5,5]]

输出： 5

解释： 选择活动 2 ，价值和为 5 。

示例 3：

输入： events = [[1,5,3],[1,5,1],[6,6,5]]

输出： 8

解释： 选择活动 0 和 2 ，价值之和为 3 + 5 = 8 。

提示：

• 2 <= events.length <= 10^5
• events[i].length == 3
• 1 <= startTimei <= endTimei <= 10^9
• 1 <= valuei <= 10^6

解题思路

使用 排序 + 后缀数组 + 二分查找 来高效解决此问题。

1. 按开始时间排序

• 首先，将所有活动按其开始时间 startTime 升序排序。
• 排序方便后续通过二分查找快速找到当前活动之后的第一个有效活动。

2. 构建后缀数组 suffixMax

• 使用后缀数组 suffixMax 保存每个活动开始后剩余活动中的最大收益，suffixMax[i] 表示从活动 i 到最后一个活动的最大收益。
• 从后往前遍历活动列表，逐步更新 suffixMax：

3. 遍历每个活动并尝试计算最大收益

• 对于每个活动 i，通过二分查找快速找到其结束时间之后开始的下一个活动。
  • 如果存在这样的活动（索引为 nextIdx），则计算收益 events[i][2] + suffixMax[nextIdx]。
  • 如果不存在，则仅考虑当前活动的收益 events[i][2]。
• 使用变量 maxSum 不断更新最大收益。

复杂度分析

• 时间复杂度：O(n log n)

  • 排序：按 startTime 排序，时间复杂度为 O(n log n)。
  • 后缀数组：构建后缀数组需要 O(n)。
  • 二分查找：对于每个活动使用二分查找，时间复杂度为 O(log n)，总共 n 次查找，因此为 O(n log n)。

• 空间复杂度：O(n)，使用了额外的后缀数组 suffixMax。

代码

/**
 * @param {number[][]} events
 * @return {number}
 */
var maxTwoEvents = function (events) {
	const n = events.length;
	// 按开始时间排序
	events.sort((a, b) => a[0] - b[0]);

	// 后缀数组，保存每个活动开始后剩余活动中的最大收益
	let suffixMax = new Array(n);
	suffixMax[n - 1] = events[n - 1][2];

	for (let i = n - 2; i >= 0; i--) {
		suffixMax[i] = Math.max(events[i][2], suffixMax[i + 1]);
	}

	let maxSum = 0; // 最大收益

	// 对于每一个事件，找到在其结束后开始的下一个事件
	for (let i = 0; i < n; i++) {
		let nextIdx = -1; // 下一个事件的 index

		// 二分查找
		let left = i + 1,
			right = n - 1;

		while (left <= right) {
			const mid = ((left + right) / 2) | 0;
			if (events[mid][0] > events[i][1]) {
				nextIdx = mid;
				right = mid - 1;
			} else {
				left = mid + 1;
			}
		}

		if (nextIdx !== -1) {
			// 如果找到有效的下一个事件，更新最大和
			maxSum = Math.max(maxSum, events[i][2] + suffixMax[nextIdx]);
		} else {
			// 如果找不到，仅考虑当前活动的收益
			maxSum = Math.max(maxSum, events[i][2]);
		}
	}

	return maxSum;
};

相关题目

题号	标题	题解	标签	难度	力扣
1235	规划兼职工作		数组 二分查找 动态规划 1+	🔴	🀄️ 🔗
1751	最多可以参加的会议数目 II		数组 二分查找 动态规划 1+	🔴	🀄️ 🔗
2555	两个线段获得的最多奖品		数组 二分查找 滑动窗口	🟠	🀄️ 🔗