跳至主要內容

2033. 获取单值网格的最小操作数

2033. 获取单值网格的最小操作数

🟠   🔖  数组 数学 矩阵 排序  🔗 力扣open in new window LeetCodeopen in new window

题目

You are given a 2D integer grid of size m x n and an integer x. In one operation, you can add x to or subtract x from any element in the grid.

A uni-value grid is a grid where all the elements of it are equal.

Return the minimum number of operations to make the grid uni-value. If it is not possible, return -1.

Example 1:

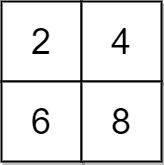
Input: grid = [[2,4],[6,8]], x = 2

Output: 4

Explanation: We can make every element equal to 4 by doing the following:

  • Add x to 2 once.
  • Subtract x from 6 once.
  • Subtract x from 8 twice.

A total of 4 operations were used.

Example 2:

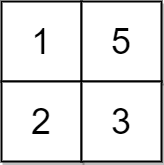
Input: grid = [[1,5],[2,3]], x = 1

Output: 5

Explanation: We can make every element equal to 3.

Example 3:

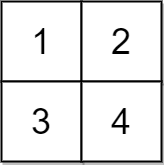
Input: grid = [[1,2],[3,4]], x = 2

Output: -1

Explanation: It is impossible to make every element equal.

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 10^5
  • 1 <= m * n <= 10^5
  • 1 <= x, grid[i][j] <= 10^4

题目大意

给你一个大小为 m x n 的二维整数网格 grid 和一个整数 x 。每一次操作，你可以对 grid 中的任一元素 加 x 或 减 x 。

单值网格 是全部元素都相等的网格。

返回使网格化为单值网格所需的 最小 操作数。如果不能，返回 -1 。

示例 1：

输入： grid = [[2,4],[6,8]], x = 2

输出： 4

解释： 可以执行下述操作使所有元素都等于 4 ：

  • 2 加 x 一次。
  • 6 减 x 一次。
  • 8 减 x 两次。

共计 4 次操作。

示例 2：

输入： grid = [[1,5],[2,3]], x = 1

输出： 5

解释： 可以使所有元素都等于 3 。

示例 3：

输入： grid = [[1,2],[3,4]], x = 2

输出： -1

解释： 无法使所有元素相等。

提示：

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 10^5
  • 1 <= m * n <= 10^5
  • 1 <= x, grid[i][j] <= 10^4

解题思路

  1. 同余性检查：

    • 若存在两个元素 a 和 b，使得 (a - b) % x !== 0，则无法通过加减 x 的倍数将它们变成相同的数，返回 -1。

  2. 选择目标数

    • 为了使总操作次数最少，应将所有数字调整到中位数，因为中位数能最小化绝对差之和。
    • 为什么是中位数？ 在一组数中，将所有数调整为中位数可最小化 |nums[i] - target| 的总和。

  3. 计算总操作次数

    • 遍历所有元素 num：
      • 计算与中位数 mid 的差值 diff = |num - mid|。
      • 如果 diff % x !== 0，则说明无法通过 x 的加减使其等于 mid，返回 -1。
      • 否则，操作次数为 diff / x，累加到 res。

  4. 返回结果

    • 如果所有元素都满足可行性条件，返回最少的总操作次数 res。

复杂度分析

  • 时间复杂度：O(m * n log (m * n))

    • 将 grid 展平成一维数组的时间复杂度为 O(m * n)。
    • 对数组排序的时间复杂度为 O(m * n log (m * n))。

  • 空间复杂度：O(m * n)，需要额外存储一维数组 nums，大小为 m * n。

代码

/**
 * @param {number[][]} grid
 * @param {number} x
 * @return {number}
 */
var minOperations = function (grid, x) {
	const nums = grid.flat(); // 将二维数组展平成一维数组
	nums.sort((a, b) => a - b); // 对数组排序

	const mid = nums[Math.floor(nums.length / 2)]; // 取中位数

	let res = 0;
	for (const num of nums) {
		const diff = Math.abs(num - mid);
		if (diff % x !== 0) return -1; // 无法通过加减x得到中位数
		res += diff / x;
	}
	return res;
};

相关题目

题号标题题解标签难度力扣
462最小操作次数使数组元素相等 II[✓]数组 数学 排序🟠🀄️open in new window 🔗open in new window