2116. 判断一个括号字符串是否有效

🟠   🔖  栈 贪心 字符串  🔗 力扣 LeetCode

题目

A parentheses string is a non-empty string consisting only of '(' and ')'. It is valid if any of the following conditions is true :

• It is ().
• It can be written as AB (A concatenated with B), where A and B are valid parentheses strings.
• It can be written as (A), where A is a valid parentheses string.

You are given a parentheses string s and a string locked, both of length n. locked is a binary string consisting only of '0's and '1's. For each index i of locked,

• If locked[i] is '1', you cannot change s[i].
• But if locked[i] is '0', you can change s[i] to either '(' or ')'.

Return true if you can makes a valid parentheses string. Otherwise, return false.

Example 1:

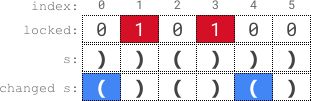
Input: s = "))()))", locked = "010100"

Output: true

Explanation: locked[1] == '1' and locked[3] == '1', so we cannot change s[1] or s[3].

We change s[0] and s[4] to '(' while leaving s[2] and s[5] unchanged to make s valid.

Example 2:

Input: s = "()()", locked = "0000"

Output: true

Explanation: We do not need to make any changes because s is already valid.

Example 3:

Input: s = ")", locked = "0"

Output: false

Explanation: locked permits us to change s[0].

Changing s[0] to either '(' or ')' will not make s valid.

Constraints:

• n == s.length == locked.length
• 1 <= n <= 10^5
• s[i] is either '(' or ')'.
• locked[i] is either '0' or '1'.

题目大意

一个括号字符串是只由 '(' 和 ')' 组成的 非空 字符串。如果一个字符串满足下面 任意 一个条件，那么它就是有效的：

• 字符串为 ().
• 它可以表示为 AB（A 与 B 连接），其中A 和 B 都是有效括号字符串。
• 它可以表示为 (A) ，其中 A 是一个有效括号字符串。

给你一个括号字符串 s 和一个字符串 locked ，两者长度都为 n 。locked 是一个二进制字符串，只包含 '0' 和 '1' 。对于 locked 中 每一个 下标 i ：

• 如果 locked[i] 是 '1' ，你 不能 改变 s[i] 。
• 如果 locked[i] 是 '0' ，你 可以 将 s[i] 变为 '(' 或者 ')' 。

如果你可以将 s 变为有效括号字符串，请你返回 true ，否则返回 false 。

示例 1：

输入： s = "))()))", locked = "010100"

输出： true

解释： locked[1] == '1' 和 locked[3] == '1' ，所以我们无法改变 s[1] 或者 s[3] 。

我们可以将 s[0] 和 s[4] 变为 '(' ，不改变 s[2] 和 s[5] ，使 s 变为有效字符串。

示例 2：

输入： s = "()()", locked = "0000"

输出： true

解释： 我们不需要做任何改变，因为 s 已经是有效字符串了。

示例 3：

输入： s = ")", locked = "0"

输出： false

解释： locked 允许改变 s[0] 。

但无论将 s[0] 变为 '(' 或者 ')' 都无法使 s 变为有效字符串。

提示：

• n == s.length == locked.length
• 1 <= n <= 10^5
• s[i] 要么是 '(' 要么是 ')' 。
• locked[i] 要么是 '0' 要么是 '1' 。

解题思路

1. 长度约束

   • 如果字符串长度 s.length 是奇数，则直接返回 false，因为有效括号字符串长度必为偶数。

2. 贪心验证

   • 从左向右遍历：
     • 用一个计数器 openCount 表示“可用的左括号数量”，包括未锁定的字符。
     • 如果遇到 '(' 或未锁定的字符 locked[i] == '0'，则 openCount++。
     • 如果遇到 ')' 并且 locked[i] == '1'，则 openCount--。
     • 如果 openCount 小于 0，说明右括号多于可用的左括号，直接返回 false。
   • 从右向左遍历：
     • 用一个计数器 closeCount 表示“可用的右括号数量”。
     • 同理，更新 closeCount，并检查是否满足条件。

复杂度分析

• 时间复杂度：O(n)，两次遍历字符串。
• 空间复杂度：O(1)，使用了常数空间来存储计数器 openCount 和 closeCount。

代码

/**
 * @param {string} s
 * @param {string} locked
 * @return {boolean}
 */
var canBeValid = function (s, locked) {
	if (s.length % 2 == 1) return false;

	let openCount = 0;
	for (let i = 0; i < s.length; i++) {
		if (s[i] == '(' || locked[i] == '0') {
			openCount++;
		} else {
			openCount--;
		}
		if (openCount < 0) return false; // 右括号过多
	}

	let closeCount = 0;
	for (let i = s.length - 1; i >= 0; i--) {
		if (s[i] == ')' || locked[i] == '0') {
			closeCount++;
		} else {
			closeCount--;
		}
		if (closeCount < 0) return false; // 左括号过多
	}

	return true;
};

相关题目

题号	标题	题解	标签	难度	力扣
20	有效的括号	[✓]	栈 字符串	🟢	🀄️ 🔗
22	括号生成	[✓]	字符串 动态规划 回溯	🟠	🀄️ 🔗
678	有效的括号字符串	[✓]	栈 贪心 字符串 1+	🟠	🀄️ 🔗
1249	移除无效的括号		栈 字符串	🟠	🀄️ 🔗
2267	检查是否有合法括号字符串路径		数组 动态规划 矩阵	🔴	🀄️ 🔗