766. 托普利茨矩阵

🟢   🔖  数组 矩阵  🔗 力扣 LeetCode

题目

Given an m x n matrix, return true if the matrix is Toeplitz. Otherwise, return false.

A matrix is Toeplitz if every diagonal from top-left to bottom-right has the same elements.

Example 1:

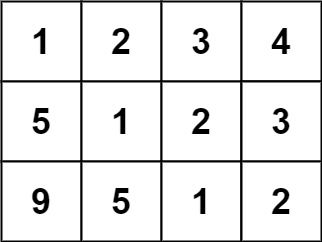
Input: matrix = [[1,2,3,4],[5,1,2,3],[9,5,1,2]]

Output: true

Explanation:

In the above grid, the diagonals are:

"[9]", "[5, 5]", "[1, 1, 1]", "[2, 2, 2]", "[3, 3]", "[4]".

In each diagonal all elements are the same, so the answer is True.

Example 2:

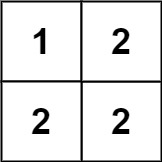
Input: matrix = [[1,2],[2,2]]

Output: false

Explanation:

The diagonal "[1, 2]" has different elements.

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 20
• 0 <= matrix[i][j] <= 99

Follow up:

• What if the matrix is stored on disk, and the memory is limited such that you can only load at most one row of the matrix into the memory at once?
• What if the matrix is so large that you can only load up a partial row into the memory at once?

题目大意

给你一个 m x n 的矩阵 matrix 。如果这个矩阵是托普利茨矩阵，返回 true ；否则，返回 __false _。_

如果矩阵上每一条由左上到右下的对角线上的元素都相同，那么这个矩阵是 __托普利茨矩阵 。

示例 1：

输入： matrix = [[1,2,3,4],[5,1,2,3],[9,5,1,2]]

输出： true

解释：

在上述矩阵中, 其对角线为:

"[9]", "[5, 5]", "[1, 1, 1]", "[2, 2, 2]", "[3, 3]", "[4]"。

各条对角线上的所有元素均相同, 因此答案是 True 。

示例 2：

输入： matrix = [[1,2],[2,2]]

输出： false

解释：

对角线 "[1, 2]" 上的元素不同。

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 20
• 0 <= matrix[i][j] <= 99

进阶：

• 如果矩阵存储在磁盘上，并且内存有限，以至于一次最多只能将矩阵的一行加载到内存中，该怎么办？
• 如果矩阵太大，以至于一次只能将不完整的一行加载到内存中，该怎么办？

解题思路

一个矩阵是 托普利茨矩阵 的条件是：任意从左上到右下的对角线上的所有元素都相等。 换句话说，对于矩阵的任意位置 (i, j)，如果其右下方的元素 (i+1, j+1) 存在，则 matrix[i][j] == matrix[i+1][j+1]。

---

基础版

1. 遍历矩阵：

   • 从第一行和第一列开始，遍历所有可能的对角线上的元素。
   • 检查是否满足 matrix[i][j] == matrix[i+1][j+1]。

2. 注意边界条件：

   • 如果是矩阵的最后一行或者最后一列，则无需再进行比较。

复杂度分析

• 时间复杂度：O(m * n)，遍历矩阵中除最后一行和最后一列的所有元素。
• 空间复杂度：O(1)，原地比较，不使用额外空间。

---

进阶版

1. 行内存加载限制：

   • 由于内存限制，一次只能加载矩阵的一行。可以采用以下策略：
     • 逐行加载矩阵，保存上一行的内容到一个数组中。
     • 加载当前行时，比较当前行与上一行相邻的元素是否相等。
     • 只需存储两行的内容，空间复杂度为 O(n)。

2. 不完整行内存限制：

   • 假设一次只能加载矩阵的一部分，可以使用滑动窗口方法。
     • 对于每次加载的一部分行或列，只记录必要的对角线元素，逐步验证其一致性。
     • 例如，可以用一个固定长度的数组存储对角线的首元素，逐步更新和比较。

复杂度分析

• 时间复杂度：O(m * n)，遍历矩阵中除最后一行和最后一列的所有元素。
• 空间复杂度：O(n)，只需存储一行的内容。

代码

基础版

/**
 * @param {number[][]} matrix
 * @return {boolean}
 */
var isToeplitzMatrix = function (matrix) {
	const m = matrix.length;
	const n = matrix[0].length;

	for (let i = 0; i < m - 1; i++) {
		for (let j = 0; j < n - 1; j++) {
			if (matrix[i][j] !== matrix[i + 1][j + 1]) {
				return false;
			}
		}
	}

	return true;
};

进阶版

/**
 * @param {number[][]} matrix
 * @return {boolean}
 */
var isToeplitzMatrix = function (matrix) {
	let prevRow = matrix[0];
	for (let i = 1; i < matrix.length; i++) {
		for (let j = 1; j < matrix[i].length; j++) {
			if (matrix[i][j] !== prevRow[j - 1]) {
				return false;
			}
		}
		prevRow = matrix[i];
	}
	return true;
};

相关题目

题号	标题	题解	标签	难度	力扣
422	有效的单词方块 🔒		数组 矩阵	🟢	🀄️ 🔗